tinyCLAP: distilling constrastive language-audio pretrained models

Francesco Paissan, Elisabetta Farella

[ pdf] [ code]


Abstract

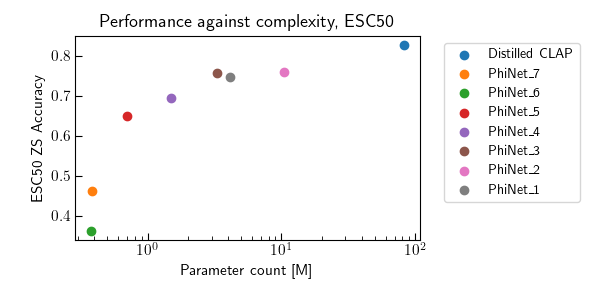
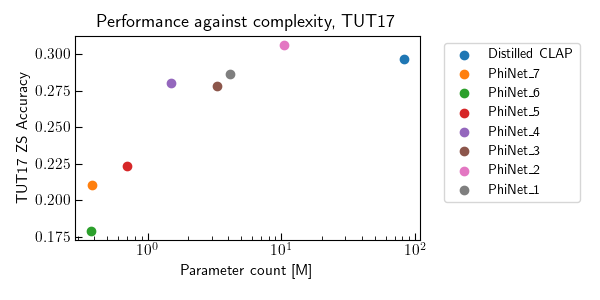
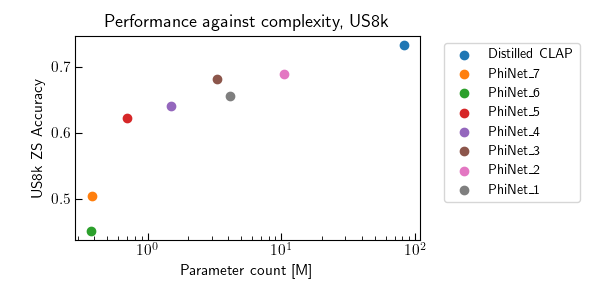
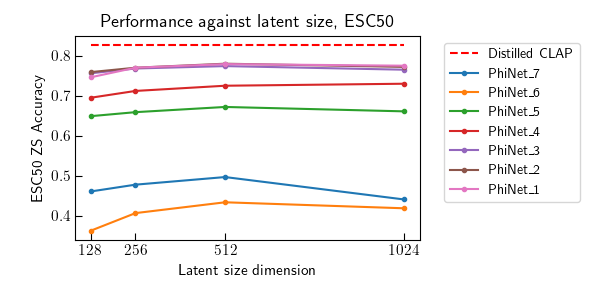
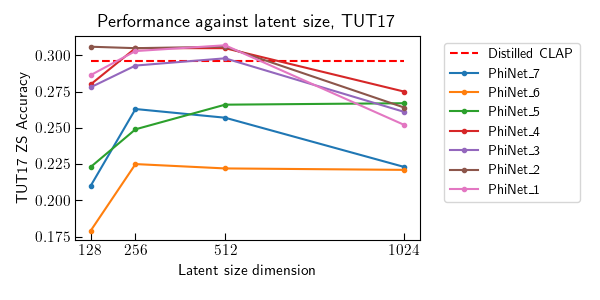
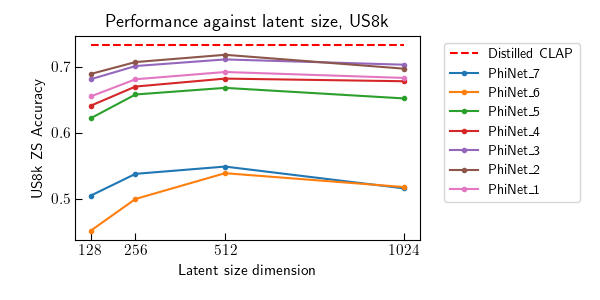
Contrastive Language-Audio Pretraining (CLAP) became of crucial importance in the field of audio and speech processing. Its employment ranges from sound event detection to text-to-audio generation. However, one of the main limitations is the considerable amount of data required in the training process and the overall computational complexity during inference. This paper investigates how we can reduce the complexity of contrastive language-audio pre-trained models, yielding an efficient model the we call tinyCLAP. We derive an unimodal distillation loss from first principles and explore how the dimensionality of the shared, multimodal latent space can be reduced via pruning. tinyCLAP uses only 6% of the original Microsoft’s CLAP parameters with a minimal reduction (less than 5%) in zero-shot classification performance across the three sound event detection datasets on which it was tested.

Contribution in a nutshell:

  • We provide a technique to distill zero-shot classifiers.
  • We benchmark the performance of CLAP after pruning the multimodal latent space.
  • We provide a technique to learn efficient CLAP models without using text data during training.

    • Play with tinyCLAP!

    Upload an audio file and write a text caption. tinyCLAP will compute the similarity score and display it in the top-right box.

    Citing tinyCLAP

    @inproceedings{paissan24_interspeech, title = {tinyCLAP: Distilling Constrastive Language-Audio Pretrained Models}, author = {Francesco Paissan and Elisabetta Farella}, year = {2024}, booktitle = {Interspeech 2024}, pages = {1685--1689}, doi = {10.21437/Interspeech.2024-193}, issn = {2958-1796}, }

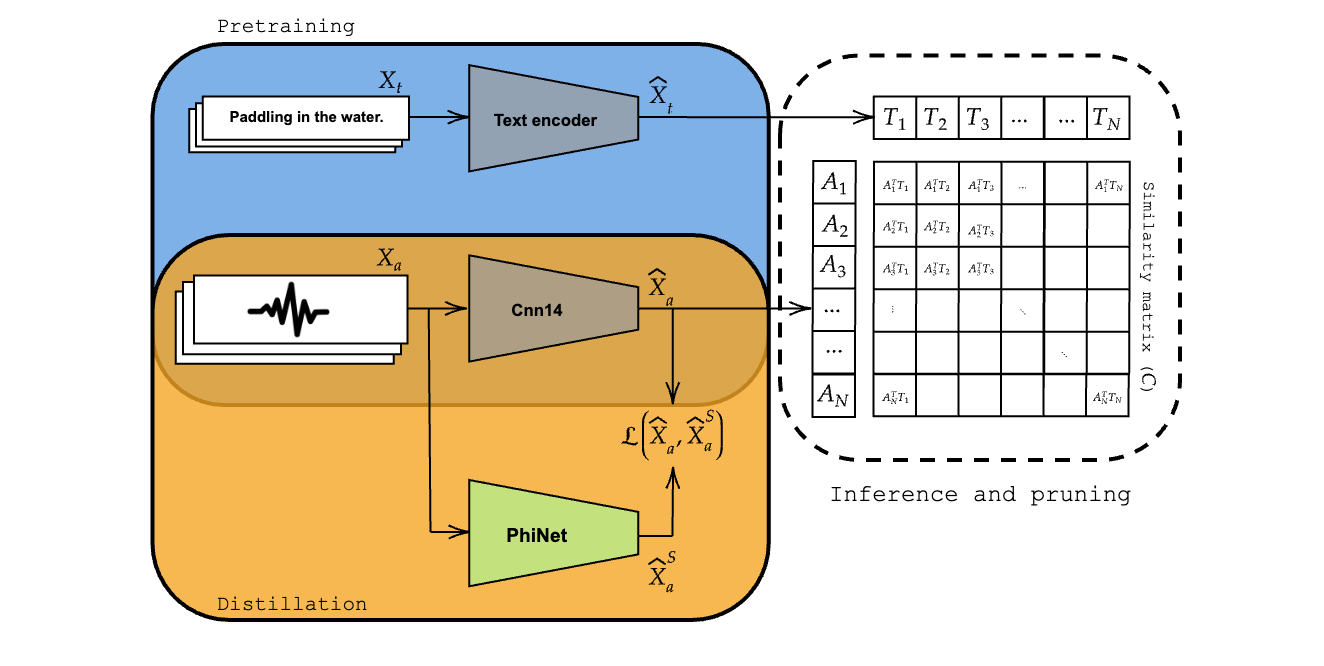
    Figure 1: To distill the teacher audio encoder, we use to loss in Equation (7) of the paper. In particular, this updates the weights of the student such that the teacher and student representations are aligned, meaning they maximum cosine distance. Therefore, they will also be aligned with the original text representations. For pruning instead, we mask-out the less contributing entries of the representations in the shared multimodal latent space. This process is described in Equation (8).


    In the paper, due to space limitations, we provided cumulative results on the three benchmarks. Hereafter, you can see the expansion of Figure 2, evaluated for each dataset independently.

    Figure 2: Performance change with respect to latent space dimension. From left to right: ESC50, TUT17, US8k. Note that for TUT17, pruning the latent space translates to a really high improvement in performance, also beating the baseline.



    Figure 3: Performance change with respect to latent space dimension. From left to right: ESC50, TUT17, US8k. Note that for TUT17, pruning the latent space translates to a really high improvement in performance, also beating the baseline.

    Finally, in this table we summarize the parameter count for all the models and latent space dimension. Considering the efficient architecture and the pruning strategy, our models span from ~400k parameters to 7M parameters.

    Params [M] ESC-50 UrbanSound8K TUT17
    r = 1024 PhiNet_7 3.3 44.1 51.6 22.3
    PhiNet_6 3.2 41.9 51.8 22.1
    PhiNet_5 3.5 66.1 65.2 26.7
    PhiNet_4 4.4 73.0 67.8 27.5
    PhiNet_3 6.2 76.5 70.3 26.1
    PhiNet_2 13.0 77.2 69.7 26.4
    PhiNet_1 7.0 77.5 68.3 25.2
    r = 512 PhiNet_7 1.4 49.7 54.9 25.7
    PhiNet_6 1.4 43.4 53.9 22.2
    PhiNet_5 1.7 67.2 66.8 26.6
    PhiNet_4 2.6 72.5 68.2 30.5
    PhiNet_3 4.3 77.4 71.1 29.8
    PhiNet_2 11.5 78.0 71.8 30.6
    PhiNet_1 5.2 77.9 69.2 30.7
    r = 256 PhiNet_7 0.7 47.8 53.8 26.3
    PhiNet_6 0.7 40.7 50.0 22.5
    PhiNet_5 1.0 65.9 65.8 24.9
    PhiNet_4 1.9 71.2 67.0 30.5
    PhiNet_3 3.5 76.8 70.1 29.3
    PhiNet_2 10.7 77.0 70.7 30.5
    PhiNet_1 4.5 77.0 68.1 30.3
    r = 128 PhiNet_7 0.4 46.1 50.5 21.0
    PhiNet_6 0.4 36.3 45.2 17.9
    PhiNet_5 0.7 64.9 62.2 22.3
    PhiNet_4 1.5 69.5 62.2 22.3
    PhiNet_3 3.3 75.6 68.1 27.8
    PhiNet_2 10.5 75.9 68.9 30.6
    PhiNet_1 4.1 74.6 65.5 28.6

    Table 2: Parameter count for different model/latent space combinations. The last row shows the marginal improvement you can get by pruning the latent space of the original CLAP model.